
Shifting the Galois output ten times to the right, we would find the same output of the Fibonacci LFSR. Just for fun, let's try it with a mirroring output. In order to obtain this kind of coupled outputs, the taps of the Galois register must be the counterparts of the ones of the Fibonacci register. Linear Feedback Shift Register in Python3. The length of the loop produced is 1 048 575, meaning we would get quite a large amount of seemingly random binary values. Say we choose a seed of 20 bits and a tap of two values, 2 and 19. The seed choice is not relevant since it would introduce only a shift in the output. The thing about shift registers is that they get pretty long, pretty quickly. In such a register, all possible states are visited - except the null state, which would make the register collapse in a sequence of 0s. I've tried so hard to crush 'em all.The two types of LFSR produce the same result - minus a reflection and a translation - when the taps are the ones generating a maximally long LFSR. I'll share it here, and if y'all got any suggestions on what I could do with it, where to send it or post it, or something, I'd appreciate that immensely! also if you see any typos.
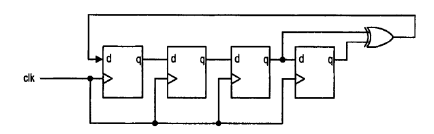
I'm hoping it's got enough of a light/goofy tone that it's worth reading. but it's written so that just about anyone with zero background could understand it. Two months later, I've got ~50 page long pdf explaining the fundamentals of computer science and RPN calculators all in service of sharing some LFSRs I wrote for the 16C. ──────────────────┬─────────────────────────Īdditionally, I was talking to a friend who's got some computer science background but doesn't mess with old HP calculators a lot, and they asked if I could write an explanation for "us dirty scrubs" and I was like, oh heck, yeah! Linear Feedback Shift Register #2 (Galois) Linear Feedback Shift Register #1 (Fibonacci)


 0 kommentar(er)
0 kommentar(er)
